Falling into a black hole: Just what do you see?
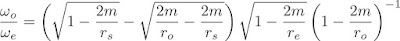
Everyone loves black holes. Immense gravity, a one-way space-time membrane, the possibility of links to other universes. All lovely stuff. A little trawl of the internets reveals an awful lot of web pages discussing black holes, and discussions about spaghettification, firewalls, lost information, and many other things. Actually, a lot of the stuff out there on the web is nonsense, hand-waving, partly informed guesswork. And one of the questions that gets asked is "What would you see looking out into the universe?" Some (incorrectly) say that you would never cross the event horizon, a significant mis-understanding of the coordinates of relativity. Other (incorrectly) conclude from this that you actually see the entire future history of the universe play out in front of your eyes. What we have to remember, of course, is that relativity is a mathematical theory, and instead of hand waving, we can use mathematics to work out what we will see. And that's what I did.
